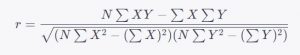Пример корреляционного анализа на основе двух переменных

Рассмотрим пример корреляционного анализа на основе двух переменных: количество часов, затраченных на учебу, и оценки студентов по их экзаменам.

Предположим, у нас есть следующие данные для 10 студентов:

Студент	Количество часов учебы (в неделю)	Оценка экзамена
A	5	80
B	3	65
C	7	90
D	2	50
E	6	75
F	4	60
G	8	95
H	1	40
I	9	100
J	5	85

Шаги корреляционного анализа:

1. Рассчитаем коэффициент корреляции Пирсона

Для этого воспользуемся формулой для коэффициента корреляции Пирсона:

где:

• $N$ — количество наблюдений (в данном случае, 10 студентов).
• $\sum XY$ — сумма произведений значений обеих переменных.
• $\sum X$ — сумма значений первой переменной (количество часов учебы).
• $\sum Y$ — сумма значений второй переменной (оценка экзамена).
• 2∑X2 — сумма квадратов значений первой переменной.
• 2∑Y2 — сумма квадратов значений второй переменной.

Посчитаем значения:

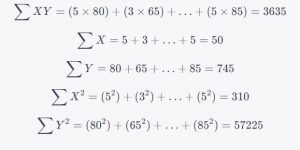
Теперь мы можем подставить эти значения в формулу и вычислить $r$:

После вычислений получаем $r\approx 0.91$.

2. Интерпретируем результаты

Коэффициент корреляции Пирсона $r$ равен приблизительно 0.91. Это значение близко к 1, что указывает на сильную положительную корреляцию между количеством часов учебы и оценкой экзамена. То есть, студенты, которые учились больше часов, обычно получали более высокие оценки на экзаменах.

3. Визуализируем результаты:

Вы также можете визуализировать эту корреляцию с помощью диаграммы рассеяния (scatter plot), на которой по оси X будет количество часов учебы, а по оси Y — оценка экзамена. В данном случае, точки на графике будут тесно сгруппированы вверх и вправо, что подтверждает сильную положительную корреляцию.

Это всего лишь пример корреляционного анализа. В реальных исследованиях вам может потребоваться использовать статистические тесты для определения статистической значимости корреляции и учитывать другие факторы, которые могут влиять на результаты.