Двухциклическое расщепление по физическим процессам — это метод численного решения уравнений Навье-Стокса, которые описывают движение вязкой несжимаемой жидкости или газа. В данном методе происходит разделение итерационного процесса на два шага, цикла или подхода для учета различных физических явлений, влияющих на поток жидкости.
Первый цикл включает только конвективные и градиентные члены уравнений Навье-Стокса, которые описывают перемещение жидкости вследствие ее инерции и давления. Этот шаг называется «чисто конвективным» и позволяет учесть основные эффекты, связанные с перемещением жидкости без учета вязкости.
Второй цикл включает вязкие члены уравнений Навье-Стокса, отвечающие за взаимодействие молекул жидкости и ее сопротивление движению. Вязкость определяет уровень трения и диссипации энергии в потоке. Этот шаг называется «чисто вязким» и позволяет учесть диффузионные эффекты в потоке.
Двухциклическое расщепление позволяет упростить численное решение уравнений Навье-Стокса и улучшить устойчивость и сходимость численных методов. Оно также облегчает параллельное вычисление, так как каждый цикл может выполняться отдельно на различных вычислительных ядрах или устройствах.
Этот метод широко применяется в численных расчетах и моделировании течений жидкостей и газов, позволяя получить аппроксимацию решения уравнений Навье-Стокса с более высокой точностью и эффективностью. Однако следует помнить, что выбор конкретного метода расщепления зависит от специфики задачи и требований к точности и скорости расчетов.
Конвективные и давительные члены являются частями уравнений Навье-Стокса, которые описывают движение жидкости или газа. Уравнения Навье-Стокса — это система уравнений для описания движения вязкой несжимаемой жидкости или газа под воздействием внешних сил и внутренних взаимодействий молекул.
Конвективные члены, также известные как «адвективные» или «переносные» члены, отвечают за учет перемещения жидкости в результате ее инерции и переноса свойств вдоль потока. Они учитывают изменение физических величин (например, скорости или температуры) в направлении течения. Конвективные члены могут привести к появлению вихрей и нестабильностей в потоке.
Пример конвективного члена в уравнениях Навье-Стокса для компоненты скорости u: (u⋅∇)u
Давительные члены, также известные как «градиентные» или «пространственные» члены, учитывают влияние давления на движение жидкости. Они связаны с изменениями давления в пространстве и влияют на изменение скорости в разных точках потока. Давительные члены играют ключевую роль в обеспечении сохранения массы и равновесия в потоке.
Пример давительного члена в уравнениях Навье-Стокса для компоненты скорости u: 
Где:
- — компонента скорости в направлении течения,
- — оператор градиента, который указывает на изменение физической величины в пространстве,
- — давление в потоке,
- — плотность жидкости или газа.
В уравнениях Навье-Стокса оба этих члена учитываются для описания сложного и нелинейного поведения потока жидкости или газа. Они играют важную роль в численных методах и моделях, используемых для решения и моделирования различных гидродинамических и аэродинамических задач.
Вязкие члены в уравнениях Навье-Стокса — это части, которые отражают влияние вязкости на движение жидкости или газа. Вязкость — это свойство жидкости или газа сопротивляться деформации и протеканию движения. Она приводит к внутреннему трению между слоями жидкости или газа, вызывая потерю энергии и приводя к затормаживанию движения.
Уравнения Навье-Стокса включают вязкие члены, чтобы учесть этот эффект. Вязкие члены связаны с градиентами скорости и являются основным механизмом, отвечающим за диффузию и диссипацию энергии в потоке. Они играют важную роль в распределении скорости в потоке и стабилизации течения.
Формы вязких членов зависят от того, какой тип движения анализируется: ламинарного или турбулентного. В ламинарных потоках вязкие члены действуют основным образом и приводят к сглаживанию скорости и установлению слоев потока. В турбулентных потоках вязкие члены служат для диссипации турбулентной энергии и стабилизации вихрей.
Пример вязкого члена в уравнениях Навье-Стокса для компоненты скорости u в трехмерном пространстве: 
Где:
- — компонента скорости в направлении течения,
- — коэффициент динамической вязкости жидкости или газа,
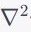— оператор Лапласа, который представляет собой вторую производную по координатам и показывает дивергенцию градиента скорости.
Вязкие члены в уравнениях Навье-Стокса играют важную роль в описании реальных течений и движений жидкости и газа. Они являются неотъемлемой частью численных методов и моделей, используемых для анализа и прогнозирования различных гидродинамических и аэродинамических явлений.
