Критерий независимости хи-квадрат (X2) является непараметрической проверкой гипотезы. Вы можете использовать его, чтобы проверить, связаны ли две категориальные переменные друг с другом.
Что такое критерий независимости хи-квадрат?
Критерий независимости хи-квадрат (X 2) является разновидностью критерия хи-квадрат Пирсона. Критерии хи-квадрат Пирсона — это непараметрические тесты для категориальных переменных. Они используются для определения того, значительно ли ваши данные отличаются от ожидаемых.
Вы можете использовать тест независимости хи-квадрат, также известный как тест ассоциации хи-квадрат, чтобы определить, связаны ли две категориальные переменные. Если две переменные связаны, вероятность того, что одна переменная имеет определенное значение, зависит от значения другой переменной.
Вычисления критерия независимости хи-квадрат основаны на наблюдаемых частотах, которые представляют собой количество наблюдений в каждой объединенной группе.
Тест сравнивает наблюдаемые частоты с частотами, которые можно было бы ожидать, если бы две переменные не были связаны. Когда переменные не связаны между собой, наблюдаемая и ожидаемая частоты будут одинаковыми.
Таблицы непредвиденных обстоятельств
Если вы хотите выполнить критерий независимости хи-квадрат, лучший способ организовать ваши данные — это тип таблицы распределения частот, называемый таблицей непредвиденных обстоятельств.
Таблица непредвиденных обстоятельств, также известная как перекрестная таблица или перекрестная таблица, показывает количество наблюдений в каждой комбинации групп. Он также обычно включает итоги по строкам и столбцам.
Тест хи-квадрат гипотез независимости
Критерий независимости хи-квадрат является логическим статистическим тестом, что означает, что он позволяет вам делать выводы о совокупности на основе выборки. В частности, он позволяет сделать вывод о том, связаны ли две переменные в совокупности.
Как и все проверки гипотез, критерий независимости хи-квадрат оценивает нулевую и альтернативную гипотезы. Гипотезы представляют собой два конкурирующих ответа на вопрос «Связаны ли переменная 1 и переменная 2?»
- Нулевая гипотеза (H 0): переменная 1 и переменная 2 не связаны в популяции; Доли переменной 1 одинаковы для разных значений переменной 2.
- Альтернативная гипотеза (H a): переменная 1 и переменная 2 связаны в популяции; Доли переменной 1 неодинаковы для разных значений переменной 2.
Вы можете использовать приведенные выше предложения в качестве шаблонов. Замените переменную 1 и переменную 2 именами ваших переменных.
Ожидаемые значения
Критерий независимости хи-квадрат работает путем сравнения наблюдаемой и ожидаемой частот. Ожидаемые частоты таковы, что пропорции одной переменной одинаковы для всех значений другой переменной.
Когда использовать критерий независимости хи-квадрат
Следующие условия необходимы, если вы хотите выполнить критерий согласия хи-квадрат:
- Вы хотите проверить гипотезу о взаимосвязи между двумя категориальными переменными (бинарными, номинальными или порядковыми).
- Критерии независимости хи-квадрат обычно выполняются для бинарных или номинальных переменных. Иногда они выполняются с порядковыми переменными, хотя обычно только с порядковыми переменными с менее чем пятью группами.
- Выборка была случайным образом отобрана из населения.
- Ожидается минимум пять наблюдений в каждой объединенной группе.
Как рассчитать тестовую статистику (формула)
Хи-квадрат Пирсона (X 2) является тестовой статистикой для критерия независимости хи-квадрат:
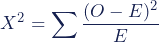
где
- Χ 2 — статистика теста хи-квадрат.
- Σ — оператор суммирования (означает «взять сумму»)
- O — наблюдаемая частота
- E — ожидаемая частота
Статистика теста хи-квадрат измеряет, насколько ваши наблюдаемые частоты отличаются от частот, которые вы ожидаете, если две переменные не связаны. Он большой, когда существует большая разница между наблюдаемой и ожидаемой частотами (O — E в уравнении).
Как выполнить тест независимости хи-квадрат
Если тестовая статистика достаточно велика, вы должны сделать вывод, что наблюдаемые частоты не соответствуют вашим ожиданиям, если переменные не связаны между собой. Но что считается достаточно большим?
Мы сравниваем тестовую статистику с критическим значением распределения хи-квадрат, чтобы решить, достаточно ли оно велико, чтобы отвергнуть нулевую гипотезу, что две переменные не связаны. Эта процедура называется критерием независимости хи-квадрат.