Т-распределение, также известное как t-распределение Стьюдента, представляет собой способ описания данных, которые следуют колоколообразной кривой при нанесении на график с наибольшим количеством наблюдений, близких к среднему, и меньшим количеством наблюдений в хвостах.
Это тип нормального распределения, используемый для небольших выборок, когда дисперсия данных неизвестна.
В статистике t-распределение чаще всего используется для:
- Найдите критические значения для доверительного интервала, когда данные примерно нормально распределены.
- Найдите соответствующее p-значение из статистического теста, использующего t-распределение (t-тесты, регрессионный анализ).
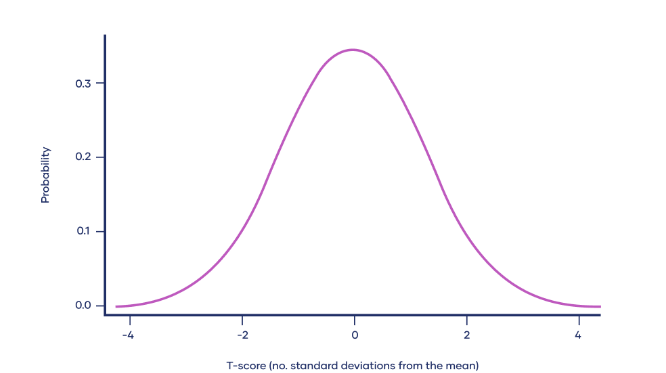
Что такое t-распределение?
Т-распределение — это тип нормального распределения, который используется для небольших выборок. Нормально распределенные данные образуют форму колокола при нанесении на график, с большим количеством наблюдений около среднего и меньшим количеством наблюдений в хвостах.
Распределение t используется, когда данные примерно нормально распределены, что означает, что данные имеют форму колокола, но дисперсия совокупности неизвестна. Дисперсия в t-распределении оценивается на основе степеней свободы набора данных (общее количество наблюдений минус 1).
Это более консервативная форма стандартного нормального распределения, также известная как z-распределение. Это означает, что оно дает более низкую вероятность центру и более высокую вероятность хвостам, чем стандартное нормальное распределение.
Т-распределение и стандартное нормальное распределение
По мере увеличения степеней свободы (общее количество наблюдений минус 1) t-распределение будет все ближе и ближе соответствовать стандартному нормальному распределению, также известному как z-распределение, пока они не станут почти идентичными.
Свыше 30 степеней свободы t-распределение примерно совпадает с z-распределением. Следовательно, z-распределение можно использовать вместо t-распределения при больших размерах выборки.
Z-распределение предпочтительнее t-распределения, когда речь идет о статистических оценках, поскольку оно имеет известную дисперсию. Он может дать более точные оценки, чем t-распределение, дисперсия которого аппроксимируется с использованием степеней свободы данных.
T-распределение и t-показатели
Т-оценка — это количество стандартных отклонений от среднего значения в t-распределении. Обычно вы можете посмотреть t-показатель в t-таблице или воспользоваться онлайн-калькулятором t-показателя.
В статистике t-показатели в основном используются для нахождения двух вещей:
- Верхняя и нижняя границы доверительного интервала, когда данные примерно нормально распределены.
- Значение p тестовой статистики для t -тестов и регрессионных тестов.
Т -показатели и доверительные интервалы
Доверительные интервалы используют t-оценки для вычисления верхней и нижней границ интервала прогнозирования. Показатель t, используемый для получения верхней и нижней границ, также известен как критическое значение t или t*.
Пример доверительного интервала. Вы выбрали 20 учащихся из двух разных классов, чтобы оценить средние результаты стандартизированного теста и хотите узнать, есть ли разница между двумя группами.
Используя двусторонний t-критерий, вы получаете оценку разницы между двумя классами и доверительный интервал вокруг этой оценки. Из t-критерия вы обнаружите, что разница в среднем балле между классом 1 и классом 2 составляет 4,61 с 95% доверительным интервалом от 3,87 до 5,35.
Поскольку доверительный интервал не пересекает ноль и на самом деле довольно далек от нуля, маловероятно, что эта разница в результатах тестов могла возникнуть при нулевой гипотезе об отсутствии различий между группами.
Т-показатели и р-значения
Статистические тесты генерируют тестовую статистику, показывающую, насколько далеки ваши данные от нулевой гипотезы статистического теста. Затем они вычисляют p-значение, которое описывает вероятность появления ваших данных, если нулевая гипотеза верна.
Статистической статистикой для t-тестов и регрессионных тестов является t-оценка. В то время как большинство статистических программ автоматически вычисляют соответствующее значение p для t-оценки, вы также можете найти значения в t-таблице, используя свои степени свободы и t-оценку, чтобы найти p-значение.
Показатель t, который генерирует значение p ниже вашего порога статистической значимости, известен как критическое значение t или t *.